Trigonometry is a branch of mathematics used to measure distance, height, or angle by applying some techniques.
Before learning some useful trigonometry formulas, here is information about the meaning of trigonometry.
Trigonometry is derived from two words of Greek, 1. “Trigonon” means “triangle” and 2. “Metron” means “measure”. And so the trigonometry is related to the study of sides and angles of a triangle.
This mathematical branch has some basic formulas list that can be beneficial for students to remember from the exam point of view.
From the school level (class 9, class 10, class 11, class 12) to competition level exams, these basic formulas of trigonometry are going to be very useful.
Useful Trigonometry Formulas
The formulas that involve trigonometric functions are called trigonometric identities. Here in this section, you can find all useful trigonometry formulas (trigonometry identity) list:
Radian and degree relation
- 180° = π radian ⇒ 1 radian = 180°/π = 57.325°
Degree and minute relation
- 1 degree = 60 minutes ⇒ 1° = 60′
- 1 minute = 60 seconds ⇒ 1′ = 60″
Basic trigonometry ratios
There are six basic trigonometry functions or ratios and the relevant formula is given below.

- sin θ =Opposite/Hypotenuse = BC/AC
- cos θ = Adjacent/Hypotenuse = AB/AC
- tan θ = Opposite/Adjacent = BC/AB
- cot θ = 1/(tan θ) = Adjacent/Opposite = AB/BC
- sec θ = 1/(cos θ) = Hypotenuse/Adjacent = AC/AB
- cosec θ = 1/(sin θ) = Hypotenuse/Opposite = AC/BC
Reciprocal identity
- sin θ = 1/cosec θ
- cos θ = 1/sec θ
- tan θ = 1/cot θ = sin θ/cos θ
- cot θ = 1/tan θ = cos θ/sin θ
- sec θ = 1/cos θ
- cosec θ = 1/sin θ
Opposite angle identity
- sin (-θ) = -sin θ
- cos (-θ) = cos θ
- tan (-θ) = -tan θ
- cot (-θ) = -cot θ
- sec (-θ) = sec θ
- cosec (-θ) = -cosec θ
Pythagorean identity
The following formulas of trigonometry are called Pythagorean identity:
- sin2 θ + cos2 θ = 1
- sec2 θ = 1 + tan2 θ
- cosec2 θ = 1 + cot2 θ
Sum and difference formula
- sin (A + B) = sin A cos B + cos A sin B
- sin (A – B) = sin A cos B – cos A sin B
- cos (A + B) = cos A cos B – sin A sin B
- cos (A – B) = cos A cos B + sin A sin B
- tan (A + B) = (tan A + tan B)/(1-tan A tan B)
- tan (A – B) = (tan A – tan B)/(1+tan A tan B)
- cot (A + B) = (cot A cot B – 1)/(cot B + cot A)
- cot (A – B) = (cot A cot B + 1)/(cot B – cot A)
‘Sum to Product’ trigonometric formulas
- sin A + sin B = 2 {sin (A + B)/2} {cos (A – B)/2}
- sin A – sin B = 2 {cos (A + B)/2} {sin (A – B)/2}
- cos A + cos B = 2 {cos (A + B)/2} {cos (A – B)/2}
- cos A – cos B = 2 {sin (A + B)/2} {sin (B – A)/2}
‘Product to Sum’ trigonometric formulas
- 2 sin A cos B = sin (A + B) + sin (A – B)
- 2 cos A sin B = sin (A + B) – sin (A – B)
- 2 cos A cos B = cos (A + B) + cos (A – B)
- 2 sin A sin B = cos (A – B) – cos (A + B)
Double angle formulas
- sin 2A = 2 sin A cos A = 2 tan A/(1 + tan2 A)
- cos 2A = cos2 A – sin2 A = 1 – 2 sin2 A = 2 cos2 A – 1 = (1 – tan2 A)/(1 + tan2 A)
- tan 2A = 2 tan A/(1 – tan2 A)
- cot 2A = (cot2 A – 1)/2 cot A
- sec 2A = sec2 A/(2 – sec2 A)
- cosec 2A = (sec A cosec A)/2
Triple angle formulas
- sin 3A = 3 sin A – 4 sin3 A
- cos 3A = 4 cos3 A – 3 cos A
- tan 3A = (3 tan A – tan3 A)/(1 – 3 tan2 A)
- cot 3A = (cot3 A – 3 cot A)/(3 cot2 A – 1)
- sec 3A = sec3 A/(4 – 3 sec2 A)
- cosec 3A = cosec3 A/(3 cosec2 A – 4)
Half angle formulas
To get the trigonometric half angle formulas, you need to replace double angle formulas 2A → A and A → A/2.
- sin A = 2 sin (A/2) cos (A/2) = 2 tan (A/2)/(1 + tan2 A)
- cos A = cos2 A/2 – sin2 A/2 = 1 – 2 sin2 A/2 = 2 cos2 A/2 – 1 = (1 – tan2 A/2)/(1 + tan2 A/2)
- tan A = 2 tan A/2/(1 – tan2 A/2)
- cot A = (cot2 A/2 – 1)/2 cot A/2
One-third angle formulas
To get the trigonometric one-third angle formulas, you need to replace triple angle formulas 3A → A and A → A/3.
- sin A = 3 sin A/3 – 4 sin3 A/3
- cos A = 4 cos3 A/3 – 3 cos A/3
Sine law
If a triangle has 3 angles A, B, and C. Where angle A faces side a, angle B faces side b, and angle C faces side c. Then the following will be the sine law or sine formula for that traingle.
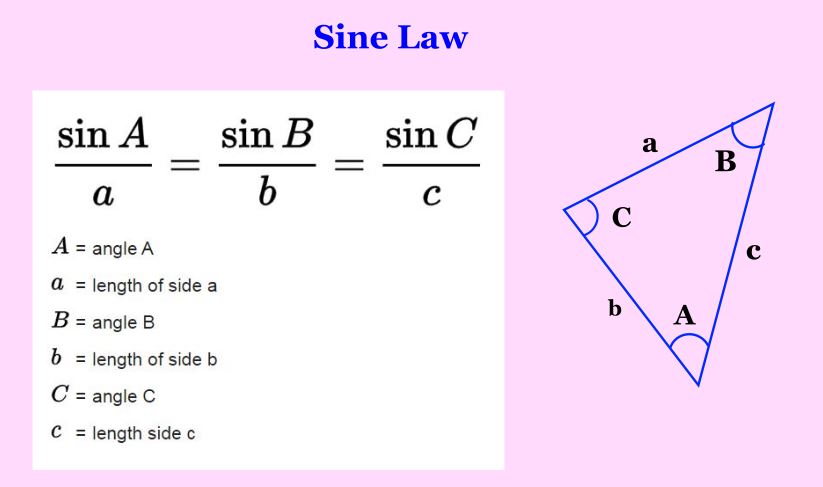
- sin A/a = sin B/b = sin C/c
- a/sin A = b/sin B = c/sin C
Cosine law
Same as “sine law” cosine law also get apply. If a triangle has 3 angles A, B, and C. Where angle A faces side a, angle B faces side b, and angle C faces side c. Then the following will be the cosine law or cosine formula for that traingle.

- a2 = b2 + c2 -2bc cos A
- b2 = c2 + a2 -2ca cos B
- c2 = a2 + b2 -2ab cos C
Inverse trigonometry formulas
If sin θ = x
⇒ θ = sin-1 x
So, if we do the inverse of a trigonometry function, we get the value of an angle. Here are mentioned some useful trigonometry formulas for inverse trigonometric identity.
- sin-1 x = cosec-1 (1/x)
- cos-1 x = sec-1 (1/x)
- tan-1 x = cot-1 (1/x)
- cot-1 x = tan-1 (1/x)
- sec-1 x = cos-1 (1/x)
- cosec-1 x = sin-1 (1/x)
Inverse opposite angle identity
- sin-1 (-x) = -sin-1 x
- cos-1 (-x) = π – cos-1 x
- tan-1 (-x) = -tan-1 x
Inverse (π/2) trigonometry formulas
- sin-1 x + cos-1 x = π/2
- tan-1 x + cot-1 x = π/2
- sec-1 x + cosec-1 x = π/2
Inverse mutual conversion trig formulas
- sin-1 x = cos-1 √(1 – x2) = tan-1 {x/√(1 – x2)}
- cos-1 x = sin-1 √(1 – x2) = tan-1 {√(1 – x2)/x}
- tan-1 x = sin-1 {x/√(1 + x2)} = cos-1 {1/√(1 + x2)}
Double angle inverse identity
- 2 sin-1 x = sin-1 {2x √(1 – x2)}
- 2 cos-1 x = cos-1 (2x2 – 1)
- 2 tan-1 x = tan-1 {2x /(1 – x2)} = sin-1 {2x /(1 + x2)} = cos-1 {(1 – x2) /(1 + x2)}
So these were the list of useful trigonometry formulas, that can be helpful for any type of competitive exam including school and college exams such as class 10, class 11, class 12, and other higher education. Also if you have any exams in 2023 then these trigonometry formulas would be really helpful.
Also Read:- Trigonometry Table: Learning Tips and Tricks

